Anyway, here’s the solution I had in mind to start with. I used A/a, B/b, and C/c to refer to the three different demographic distinctions.
 [Shortly after I composed this post, Brian sent me a description of this solution; he was the only person to do so.] But here’s a much simpler solution, a version of which was first submitted by Chris Fulmer:
[Shortly after I composed this post, Brian sent me a description of this solution; he was the only person to do so.] But here’s a much simpler solution, a version of which was first submitted by Chris Fulmer: This solution, like many others (including those suggested by Patri Friedman and Chris Hibbert), relies on an up/down, left/right, inside/outside principle for segregating the groups. It doesn’t meet the “landlocking” condition that I added later, but when I added that condition, Chris responded by just taking one of the outside territories and wrapping it around all the others:
This solution, like many others (including those suggested by Patri Friedman and Chris Hibbert), relies on an up/down, left/right, inside/outside principle for segregating the groups. It doesn’t meet the “landlocking” condition that I added later, but when I added that condition, Chris responded by just taking one of the outside territories and wrapping it around all the others: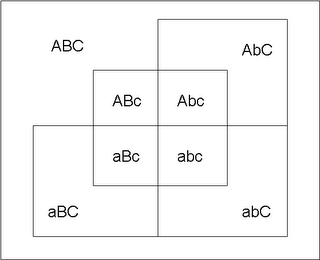 And then I began wondering if there was any reasonable set of conditions that would make my solution unique. Blar, who had submitted a solution essentially the same as my own, but using triangles instead of circles...
And then I began wondering if there was any reasonable set of conditions that would make my solution unique. Blar, who had submitted a solution essentially the same as my own, but using triangles instead of circles... ...suggested adding a condition that no territory touches more than three other territories (not including corner meetings). But the second solution above already satisfies that criterion. The third solution doesn’t satisfy the border-only-three criterion, but it does satisfy landlocking. So maybe we could impose both border-only-three and landlocking? Nope. Blar sent the following variation on the third solution above that meets both additional criteria:
...suggested adding a condition that no territory touches more than three other territories (not including corner meetings). But the second solution above already satisfies that criterion. The third solution doesn’t satisfy the border-only-three criterion, but it does satisfy landlocking. So maybe we could impose both border-only-three and landlocking? Nope. Blar sent the following variation on the third solution above that meets both additional criteria: What’s the bottom line? I think Blar gets it right: “All of these solutions are identical in terms of what territories are touching - the only difference besides topologically irrelevant shape-changing is what's touching walls.” And it’s not hard to modify any given layout to meet whatever wall-touching (landlocking) condition you want. I conclude that there’s probably no way to force my solution without a giveaway condition like, “Must use overlapping circles.” Ah, well.
What’s the bottom line? I think Blar gets it right: “All of these solutions are identical in terms of what territories are touching - the only difference besides topologically irrelevant shape-changing is what's touching walls.” And it’s not hard to modify any given layout to meet whatever wall-touching (landlocking) condition you want. I conclude that there’s probably no way to force my solution without a giveaway condition like, “Must use overlapping circles.” Ah, well.ALSO: The computing background of many readers shone through in their choice to represent demographic categories using binary notation (000 = black male young, 001 = black male old, etc.). But one reader, Ben, used colors instead:
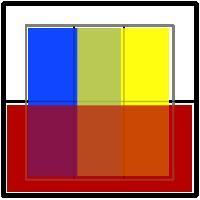 Primary colors (blue, red, yellow) represent pure categories (black, female, old), and absences of those colors represent their opposites. All the other colors are category combinations – e.g., green = yellow + blue = old black male. I don't know if this approach aids understanding, but I like it anyway.
Primary colors (blue, red, yellow) represent pure categories (black, female, old), and absences of those colors represent their opposites. All the other colors are category combinations – e.g., green = yellow + blue = old black male. I don't know if this approach aids understanding, but I like it anyway.
3 comments:
You can characterize these solutions as “deformations of an octahedron” ... but I don’t know how to prove that that’s a complete characterization of the solution set.
The following observation was fun: Imagine slicing a beach ball along three perpendicular axes. Depending on how you projected the resulting figure onto the plane, you could get any of the first four pictures fairly naturally. One controlling parameter is whether you assign the center of the projection to a face (pictures 1 and 4) or a corner (2 and 3). Another parameter is whether you assign the point at infinity to a face (picture 3) or omit it (2).
If you projected the beach ball from a face, you get picture 1 (Glen's original). If you "sharpen" the beach ball into an octahedron before projection, you get 4.
Conveniently, the beach ball/octahedron solution could be characterized as "overlapping circles".
(After Ben's colored solution was added to the post, I had to update my comment.)
For the octahedral characterization to be complete, one would have to allow deformation of intersections into edges – more precisely, declare any vertex where four edges meet equivalent to two three-edge vertices with a common edge. Deforming a four-way intersection into an edge in this way adds another connection between the faces and destroys none, so splitting the vertices of one solution yields another solution. Armed with this equivalence we can generate Ben's colored solution, which is otherwise not strictly topologically equivalent to the octahedron because some of the faces he drew have four neighbors.
So far every solution posted fits this characterization, but I still don't know if it's complete.
FXKLM --
You scared me!
When Glen says "a set must be contiguous", he means that there is a path from any one member of the set to any other member of the set that passes only through faces (not vertices) and does not pass through any member not in the set. True, the two faces you point out do not touch, but the should-be-contiguous set to which they belong, namely, the set of faces with capital C, is in fact contiguous.
Post a Comment